
Mathematical Sciences
Numerical Models for Inertial-Electrostatic Confinement Fusion
Team Member(s)
Nico BraukmanFaculty Advisor
Dr. Vladislav BukshtynovNumerical Models for Inertial-Electrostatic Confinement Fusion File Download
Project Summary
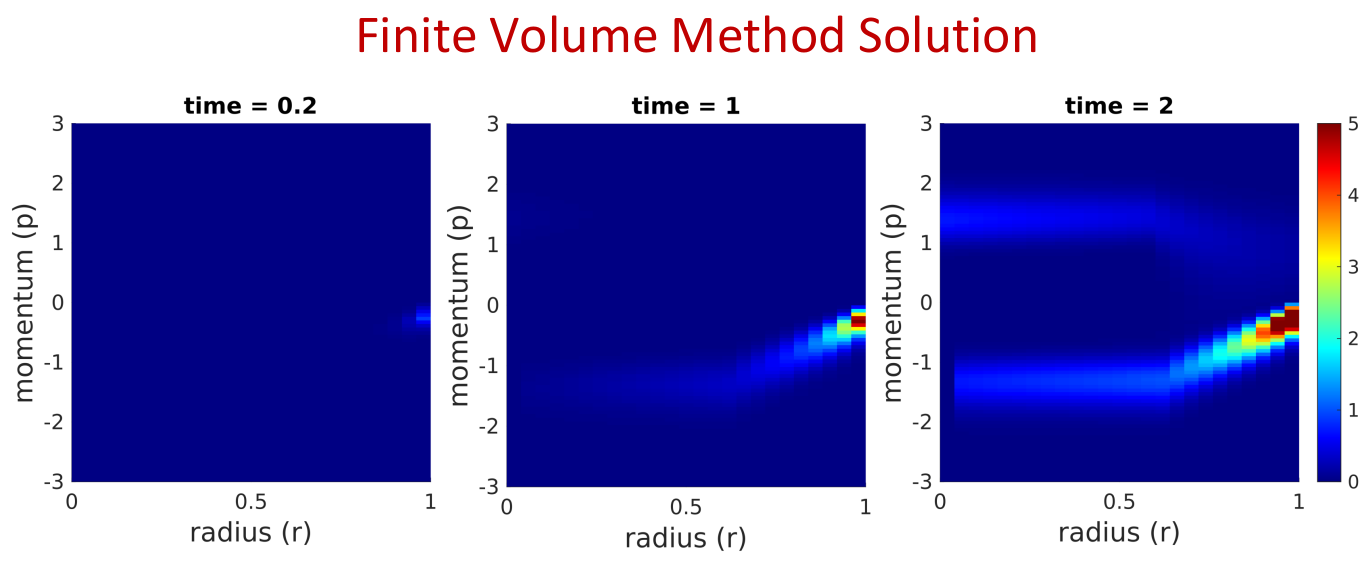
Inertial-Electrostatic Confinement (IEC) fusion devices trap plasma ions with a spherically symmetric electrostatic field that accelerates ions inward, where they collide and fuse. IEC devices are simple to construct, and using them to study plasma motion will help advance fusion energy research. Here, plasma motion in an IEC device is numerically simulated by solving the Vlasov-Poisson equations using the finite volume method (FVM) and finite element method (FEM). The device consists of an outer positively-charged mesh (the anode) and an inner negatively-charged mesh (the cathode). Ions are injected into the device at the anode with small initial momentum. They are accelerated along the electric field to the cathode, then continue with constant momentum toward the center of the device. The ions that do not fuse continue to the opposite side, slowing down as they move against the electric field, and eventually reach a turning point and fall back to the center for another chance to fuse. The Vlasov-Poisson equations describe the time evolution of a collisionless plasma in an electrostatic field. For a spherically symmetric system, the equations simplify to one dimension of space and one dimension of momentum. The Vlasov equation describes how the phase-space density of ions changes due to the electric field, and the Poisson equation describes how the electric field changes due to the presence of ions. In the FVM, the Vlasov equation is solved over a discretized domain by computing the flux of ions across the boundaries of each sub-cell. The electric field is computed using Gauss’ law, which gives a solution to the Poisson equation. The FVM solution computed in MATLAB shows the expected ion motion. In the FEM, the Vlasov and Poisson equations are solved in their weak forms over piecewise linear (P1) and piecewise constant (P0) finite element spaces, respectively, using the FreeFEM PDE solving software. The FEM solution shows qualitatively similar ion motion to the FVM solution, however, the term describing the injection of ions introduces errors in the FEM solution which accumulate over time.Future Works
In future simulations, spectral methods for solving the Vlasov-Poisson equations will b investigated as an alternative to the FVM or FEM.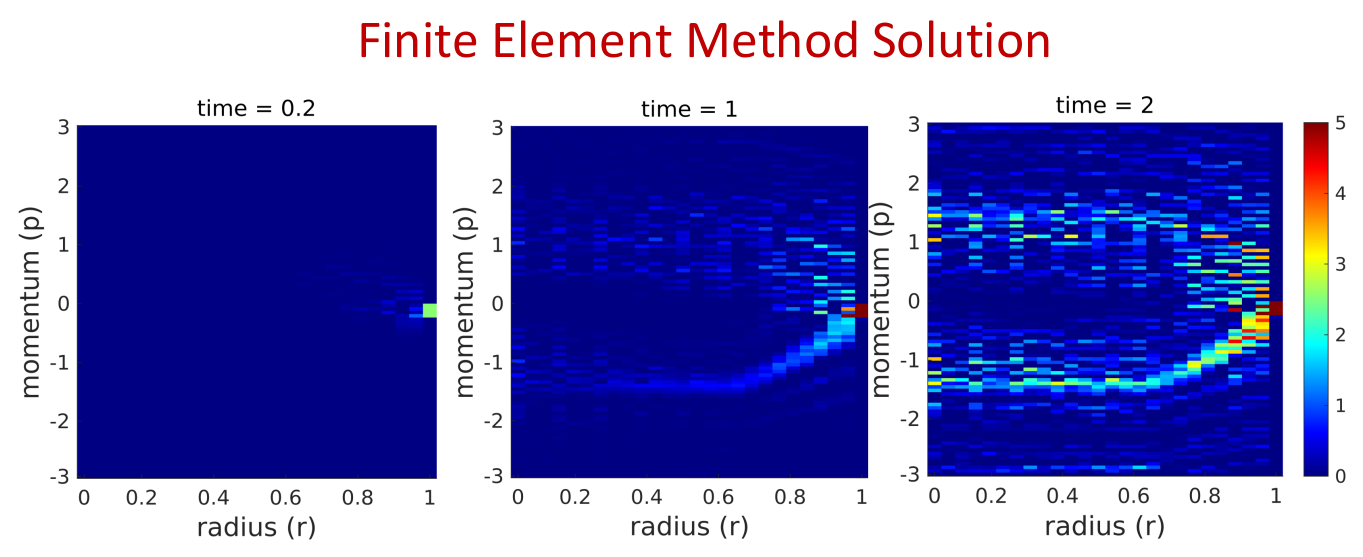
Testing the Relativistic-Microwave Theory of Ball Lightning with Plasma Simulations
Team Member(s)
Amanda ElliottFaculty Advisor
Dr. Vladislav Bukshtynov, Dept. of Mathematical Sciences, Florida TechTesting the Relativistic-Microwave Theory of Ball Lightning with Plasma Simulations File Download
